En esta publicación te presentamos una de las distribuciones
de muestreo más utilizadas: La distribución Normal muy útil en la estadística.
¿En qué consiste la Distribución Normal?
Es una de las más
importantes y ocupadas en la “inferencia
estadística”, debido a que las distribuciones de muchas muestras aleatorias
tienden hacia la distribución normal conforme aumenta el tamaño de la muestra.
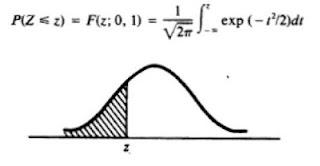
La forma grafica de la distribución Normal es una curva simétrica con forma de
campana, que se extiende sin limite tanto en la dirección positiva como
negativa.
Algunos ejemplos donde se
ocupa la distribución normal son por ejemplo los datos meteorológicos tales
como la temperatura y la precipitación, calificaciones de actitud, etc.
Definición: Se dice que
una variable aleatoria X se encuentra normalmente distribuida si su función de
densidad está dad por:
Los parámetros de
distribución normal son μ que
corresponde a la media de “x” y σ que es la desviación estándar de x.
Finalmente para
simplificar el uso de la distribución normal se utiliza la siguiente
transformación:
Z es una variable
aleatoria estandariza con media cero
y desviación estándar uno.
Teorema:
Sea X1, X2,
X3,… Xn un conjunto de variables aleatorias independientes normalmente distribuidas con medias E(Xi) y varianza (Xi) = σ2, para i = 1,2,…n.
Entonces:
En donde α1, α2...αn
son constantes, entonces Y también es una variable
aleatoria con distribución normal y media.
La distribución de Muestreo
Esta estadística tiene un papel importante cuando las medias poblacionales son desconocidas.
Sea X1, X2,
X3,…Xn una muestra
aleatoria que consiste en n variables aleatorias tales que;
E (Xi) = μ y Var (i) = σ2
para todo i =1,2,…n.
Entonces "X" = (X1+X2+X3+…+Xn)/n
se define como la media de n variables
aleatorias.
Entradas Relacionadas
Otras entradas relacionadas sobre estadísticas que pueden interesarte las puedes visitar haciendo clic en los siguientes
post:
- Estadística descriptiva
- Distribución t student
- Ejercicio de distribución Normal
- Medida de Apuntamiento o Curtosis
Material relacionado para descargar
Material complementaria a
tema de estudio en el siguiente enlace:




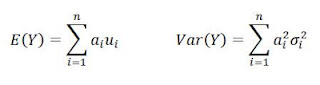



No hay comentarios:
Publicar un comentario