En esta ayudantía
enseñamos el método del Factor Integrante para la resolución
de ecuaciones
diferenciales, también a modo de ejemplo un ejercicio resuelto.
Método del Factor Integrante
Solución
de Ecuaciones
Diferenciales mediante el método de Factor Integrante:
La condición es que P(X) y Q(x) sean Ecuaciones Continuas
Ejercicio de Factor Integrante
Resolver la siguiente ecuación diferencial mediante el Método
de Factor
Integrante:
Desarrollo
Primero es debe estandarizar la ecuación diferencial de
fácil visualización para aplicar el método:
Entradas Relacionadas
Otras entradas relacionadas que pueden interesarte las puedes visitar
haciendo clic en los siguientes post:
- Separación de Variables (Ecuaciones Diferenciales)
- Solución de Ecuaciones de Diferencias lineales Homogéneas
- Solución de Ecuaciones Diferenciales lineales Homogéneas
- Ecuaciones de diferencia lineales no homogéneas
- Ecuaciones diferenciales no homogéneas
Bibliografía Relacionada
Bibliografía
complementaria a tema de estudio en el siguiente enlace:
- Libros y material de Algebra (Pruebas, apuntes, ejercicios resueltos)
- Libro Introducción al Álgebra Lineal




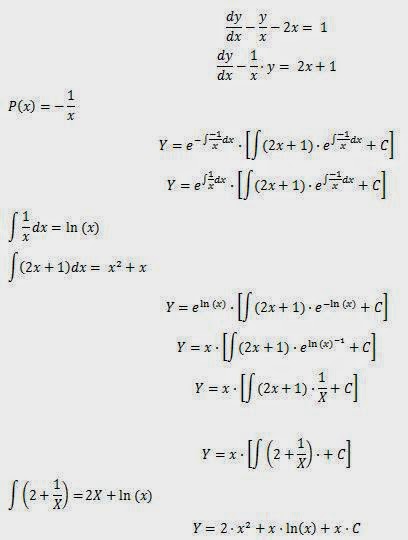


No hay comentarios:
Publicar un comentario