En esta ayudantía de ecuaciones diferenciales aprenderás
a encontrar la solución de Ecuaciones de Diferencias lineales Homogéneas; con un
ejemplo resuelto.
Resolución de Ecuaciones de Diferencias lineales Homogéneas
Ecuación característica:
Solución homogénea
Solución general
Ejercicio
1. x(k+2)
= 6x(k+1)-8(k); x(0) = x(1) = 2
Desarrollo
1. x(k+2)
= 6x(k+1)-8(k); x(0) = x(1) = 2
Se reemplazan en la ecuación las condiciones iniciales
para saber el valor de c1 y c2.
Resolviendo
el sistema de ecuaciones se tiene que c1
= -1 y c2 = 3.
Entradas Relacionadas
Otras entradas relacionadas que pueden interesarte las puedes visitar
haciendo clic en los siguientes post:
- Separación de Variables (Ecuaciones Diferenciales)
- Factor Integrante (Ecuaciones Diferenciales)
- Solución de Ecuaciones Diferenciales lineales Homogéneas
- Ecuaciones de diferencia lineales no homogéneas
- Ecuaciones diferenciales no homogéneas
Bibliografía Relacionada
Bibliografía
complementaria a tema de estudio en el siguiente enlace:
- Libros y material de Algebra (Pruebas, apuntes, ejercicios resueltos)
- Libro Introducción al Álgebra Lineal





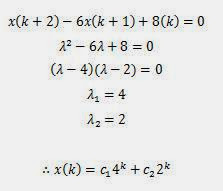
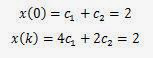


No hay comentarios:
Publicar un comentario